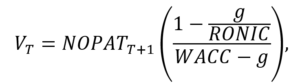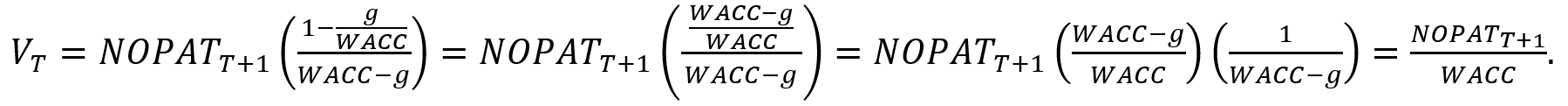Recent appraisal actions before the Delaware Court of Chancery highlight the need for clarity about the assumptions—both explicit and implicit—in the terminal value component of discounted cash flow (“DCF”) models used for the valuation of companies. Terminal value is the lump-sum discounted value of all cash flows expected to occur after the explicit forecast period.
Consistent with basic economic and finance principles, the terminal value should increase with growth only if the firm can earn a return on capital in excess of its cost of capital (i.e., positive net present value projects). Because such opportunities over the longer term are limited in a competitive market, valuation models that are highly sensitive to the assumed growth rate should be treated with caution, as they likely embed unrealistically optimistic assumptions about value creation.
In an October 2022 decision in Ramcell, Inc. v. Alltel Corp., the court determined the fair value of Jackson Cellular Telephone Co. (“Jackson”) when it was acquired by Alltel Corporation on April 4, 2019.[1] In its ruling, the court calculated Jackson’s terminal value using the so-called convergence model,[2] which explicitly links growth, investment, and return on investment. The court reasoned that although Jackson was likely to experience continued growth in the long term, “[t]here is no free growth, and, in this case, the court finds that the terminal value model should make this concept explicit.”[3]
Ramcell was certainly not the first time that valuation experts have presented the convergence model in the Delaware Court of Chancery. The model has been used in multiple appraisal actions over the past decade, and we find it used in cases dating back to 1990.[4] However, the Court of Chancery has not universally accepted the convergence model. For example, the recent revised ruling in HBK Master Fund v. Pivotal Software, Inc. rejected the convergence approach, finding that it inappropriately “implemented an effective 0% perpetuity growth rate in the terminal period” when a 2.5 percent growth rate was warranted.[5]
In this article, we discuss the convergence approach and its implications for growth assumptions in DCF models.
Background on Terminal Value Calculations
DCF models calculate the present value sum of the expected future cash flows of a business. Experts preparing DCF models typically start by examining financial projections from company management or third parties. Company projections often extend only a few years into the future, however. To capture the value of cash flows beyond the projection period, experts estimate a terminal value that reflects the lump-sum equivalent of all future cash flows after the period for which actual projections exist. In many DCF models, a significant portion of the subject firm’s estimated value is attributable to the terminal value.[6] Embedded within the terminal value are explicit or implicit assumptions about the company’s future profits, growth, risk, and investment needs. These assumptions must be internally consistent. In particular, the investment rate—the fraction of after-tax profits that the company reinvests—will depend on the profitability and rate of growth.
One popular technique for estimating the terminal value involves extrapolating future cash flows from the final year of the projections at a constant long-term growth rate. Under this approach, the subject business’s profit margins, tax rate, and investment rate in the final year of the projections are assumed to remain constant in perpetuity. The simplicity of the approach has great appeal, and, unsurprisingly, its use is widespread. A 2006 survey of corporate financial advisers and private equity professionals, for example, found that 80 percent of participants used the extrapolation approach to estimate terminal value.[7] The extrapolation approach is also prominent in popular reference books for investment banking professionals.[8]
Despite its popularity, the extrapolation approach is problematic when there is a mismatch between the projected investment rate and the long-term constant growth rate chosen by the expert.[9] As the court correctly observed in Ramcell, growth is not free. Instead, growth requires investment, and competition will tend to prevent continued returns in excess of the cost of capital. Thus, low investment but high growth yields an implausibly high return on investment. In Ramcell, for example, a terminal value calculation prepared by the petitioners’ expert using the extrapolation approach implied a return on investment ranging from 193 percent to 227 percent—more than ten times what is plausible in a competitive industry.[10] The court credited an illustration of this fact prepared by the respondent’s expert in electing to adopt the convergence approach instead.[11]
The Convergence Approach
The convergence approach, in contrast, explicitly constrains the subject firm’s long-run return on investment to a reasonable target rate. Often, a reasonable return on investment is the firm’s cost of capital—that is, the return that investors expect after paying for all the costs associated with operating the business.[12] This is because a business consistently earning returns that exceed its cost of capital (thus increasing the value of the business) will tend to attract vigorous competition. Competition, in turn, will exert downward pressure on the company’s return on investment.[13] For example, a competitor may need only reduce its prices a bit to steal market share and capture some of the “spread” between returns and capital costs in the industry. Outsized profits will also attract new entrants. As a result, excess returns—the spread between return on investment and the cost of capital—should disappear in the long run for competitive industries.
While the convergence approach assumes that a company’s excess returns will (slowly) dissipate, growth in revenue and profits is another matter. Under the convergence approach, a company may continue growing even while its excess returns disappear. The subtlety arises from the distinction between growth and value creation. When a company’s return on investment equals its cost of capital, growth does not create extra value because the cost of funding that growth just offsets the benefit. Two simple examples are investments in projects with zero net present value and an acquisition at a price that reflects the full value of the target. It is only when a company’s return on investment exceeds its cost of capital that growth creates value. On the other hand, growth reduces value when the cost of capital exceeds the return on investment. Thus, while the formula for the convergence model calculates terminal value as if the firm has no growth, it is more precise to say that the firm is growing but the cost of funding that growth offsets the benefit.[14]
Every Terminal Value Calculation Embeds an Assumption about Long-Term Investment
Careful readers may object that tying the long-term return on investment to the cost of capital requires projecting a firm’s investment expenditures far into the future. In the Pivotal decision, for example, the court inferred that “[t]rying to ascertain a plowback ratio a decade from the valuation date appears speculative at best, at least under these facts.”[15] While projecting the plowback ratio a decade out may appear speculative, other techniques for calculating terminal value also implicitly embed an assumed plowback ratio.
Consider, for example, the extrapolation approach discussed above. The extrapolation approach grows projected cash flows at a constant rate in perpetuity. Cash flow equals after-tax profits less investment, by definition, so the extrapolation approach inherently includes a specific, constant-growth projection of investment far into the future. The distinction is not that one terminal value calculation approach requires projecting investment and the other does not. By virtue of what the terminal value represents—the present value of a stream of cash flows—both terminal value approaches embed projections of long-term investment. Instead, what distinguishes these approaches is the nature of the specific investment projection and what it implies for other variables of interest, like return on investment. Under the convergence approach, the investment projection imposes economic discipline arising from competitive market conditions in setting the long-term return on investment in relation to the cost of capital. That modeling structure avoids unrealistic scenarios that often arise under the extrapolation approach, where investment returns significantly exceed the cost of capital forever, giving rise to an inflated valuation that is inconsistent with a competitive market.
Conclusion
Growing recognition of the merits of the convergence approach in valuation practice and case law puts the assumptions embedded in alternative approaches in sharp relief. Experts adopting alternative approaches, such as the extrapolation approach, are likely to face heightened scrutiny about whether the often-implicit assumptions embedded in their terminal value calculations are consistent with reasonable expectations for long-run market conditions. On the other hand, experts adopting the convergence approach may face challenges about the competitive forces driving up long-run investment requirements relative to management’s near-term expectations as reflected in company projections.
Disclosure: Michael Cliff was a member of the Analysis Group teams that supported valuation experts for the respondents in the PetSmart, Solera, and Jarden cases cited in the endnotes. Joseph Maloney was a member of the Analysis Group teams that supported valuation experts for the respondents in the PetSmart and Jarden cases. The opinions expressed are those of the authors and do not necessarily reflect the views of Analysis Group or its clients.
Ramcell, Inc. v. Alltel Corp., No. 2019-0601-PAF, 2022 WL 16549259, at *1 (Del. Ch. Oct. 31, 2022). ↑
Id. at *27–28. This model is also referred to as the “plowback,” “value-driver,” or “McKinsey” model. ↑
Id. at *28. ↑
See, e.g., Cede & Co. v. Technicolor, No. 7129, 1990 Del. Ch. LEXIS 259, at *86 (Del. Ch. Oct. 19, 1990); In re John Q. Hammons Hotels S’holder Litig., No. 758-CC, 2011 Del. Ch. LEXIS 1, at *15 (Del. Ch. Jan. 14, 2011); In re PetSmart, Inc., 2017 Del. Ch. LEXIS 89, at *86 (Del. Ch. May 26, 2017); In re Appraisal Solera Holdings, Inc., 2018 Del. Ch. LEXIS 256, at *75 (Del. Ch. July 30, 2018); In re Appraisal of Jarden Corp., 2019 Del. Ch. LEXIS 271, at *83, *89 (Del. Ch. July 19, 2019); In re Panera Bread Co., No. 2017-0593-MTZ, 2020 Del. Ch. LEXIS 42, at *97 (Del. Ch. Jan. 31, 2020). ↑
HBK Master Fund L.P. v. Pivotal Software, Inc., No. 2020-0165, 2024 Del. Ch. LEXIS 332, at *3 (Del. Ch. Mar. 12, 2024). ↑
See, e.g., Tim Koller, Marc Goedhart & David Wessels, Valuation: Measuring and Managing the Value of Companies 285–86 (John Wiley & Sons 7th ed. 2020). ↑
Christian Petersen, Thomas Plenborg & Finn Schøler, Issues in Valuation of Privately Held Firms, 10 J. Private Equity, at exhibit 7 (2006). ↑
Stephen Ross, Randolph Westerfield & Bradford Jordan, Fundamentals of Corporate Finance: A Handbook 165–67 (McGraw-Hill 12th ed. 2019); see also Joshua Rosenbaum & Joshua Pearl, Investment Banking: Valuation, Leveraged Buyouts, and Mergers & Acquisitions 132–33 (John Wiley & Sons 2009). ↑
To be clear, extrapolation per se is not the issue. The problem arises when extrapolating from projections that do not reflect a sustainable relationship between growth, profitability, and reinvestment. ↑
Ramcell, Inc. v. Alltel Corp., No. 2019-0601-PAF, 2022 WL 16549259, at *28 (Del. Ch. Oct. 31, 2022). ↑
Id. ↑
See Richard A. Brealey, Stewart C. Myers & Franklin Allen, Principles of Corporate Finance 292 (McGraw-Hill 13th ed. 2020) (“Profits that more than cover the cost of capital are known as economic rents. Economics 101 teaches us that in the long run, competition eliminates economic rents. That is, in a long-run competitive equilibrium, no company can expand and earn more than the cost of capital on that investment.”). ↑
Some valuation professionals allow for a spread above the cost of capital when determining the long-run return on investment. See Aswath Damodaran, The Dark Side of Valuation: Valuing Young, Distressed, and Complex Businesses 286 (Pearson 2d ed. 2010) (noting that, in some cases, a spread between the long-term return on investment and the cost of capital of up to 4 percent or 5 percent could be warranted). ↑
The general formula for terminal value under the convergence model is:

where g is the terminal growth rate in after-tax operating profits (NOPAT), RONIC is the return on new invested capital, and WACC is the weighted average cost of capital. This valuation formula clearly allows for nonzero growth. However, when the return on new invested capital equals the weighted average cost of capital, the growth rate cancels out of the formula:

The firm is growing at the rate g, but with a “lower” cash flow base that reflects an investment rate of g / WACC. The value of this growing firm is equivalent to another firm with no investment (and therefore a higher cash flow base) and no growth. ↑
HBK Master Fund L.P. v. Pivotal Software, Inc., No. 2020-0165, 2024 Del. Ch. LEXIS 332, at n.478 (Del. Ch. Mar. 12, 2024). ↑